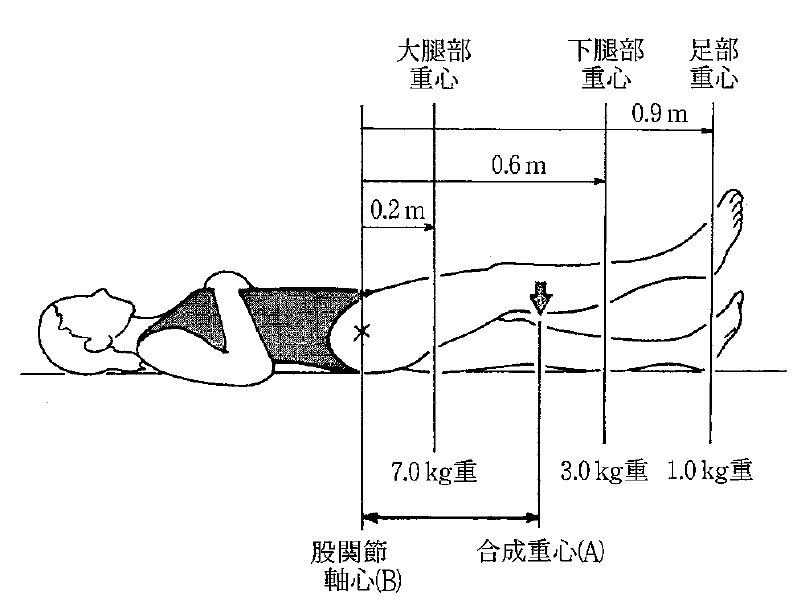
5. 背臥位で右下肢挙上位を保持している図を示す。各部の重量、重心位置、股関節軸心からの水平距離を示している。
下肢の合成重心(A)から股関節軸心(B)までの距離を求めよ。
ただし、小数点以下第3位を四捨五入する。
1. 0.31m
2. 0.34m
3. 0.37m
4. 0.40m
5. 0.43m
目次
【解説】
合成重心の求め方
(質量1×原点から物体1までの距離)+(質量2×原点から物体2までの距離)+(質量3×原点から物体3までの距離)・・・
という風に、
(物体の質量×物体の原点からの距離)を合計します。
そして、その値を
全重量 すなわち (物体1+物体2+物体3+・・・)で割ると重心の位置が出てきます。
具体的には?
下図のように3つの物体の合成重心を求める場合を考えてみましょう。
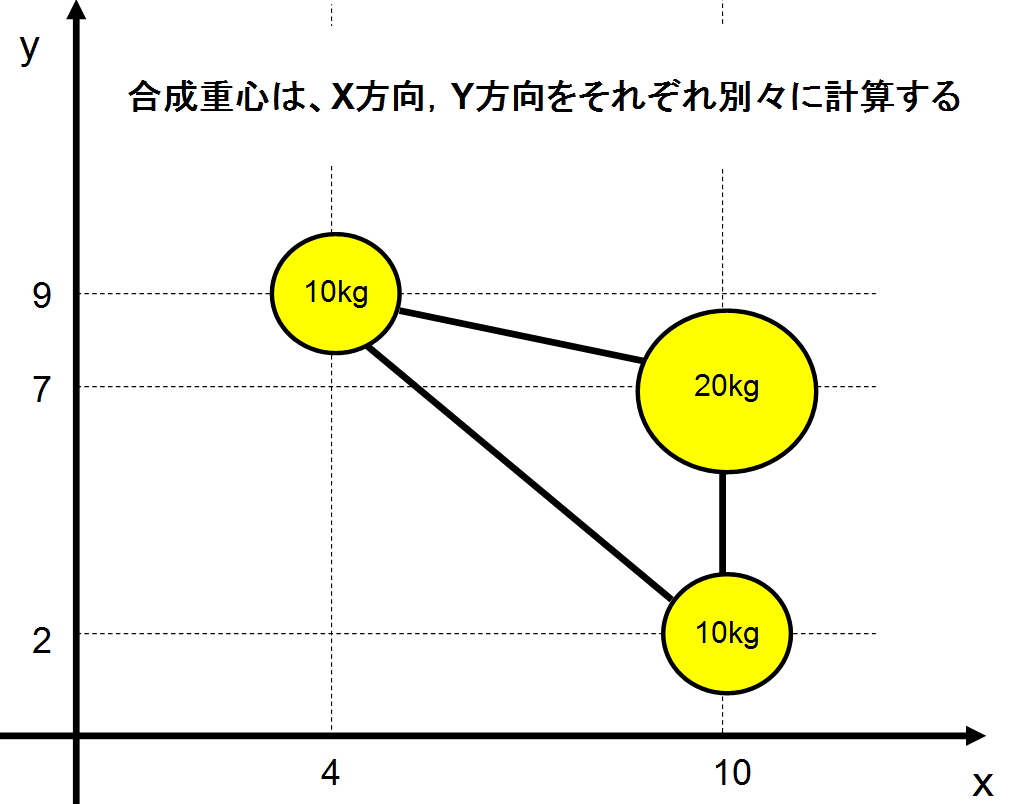
この合成重心の位置は、
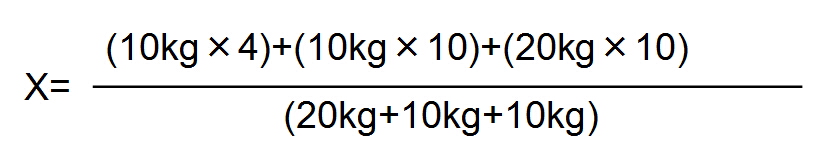

X軸=8.5
Y軸=6.25
で(X,Y)=(8.5、6.25)となります。
本題については?
求める下肢の合成重心までの距離は、BAです。
上の説明を元に考えると、
BAはX軸となります。Bの位置を原点として考えると、
今回はX軸だけ考えて出せば良いということになります。
合成重心の出し方に従って、今回のX軸の値を求めると
大腿部重心までの距離が0.2m、質量が7kg
下腿部重心までの距離が0.6m、質量が3kg
足部重心までの距離が0.9m、質量が1kg
なので、
(7×0.2)+(3×0.6)+(1×0.9)を
全体の重量=7+3+1
で割れば(除すれば)答えがでます。
計算すると、0.37となります。
答え
3.(0.37)
