40 極超短波治療の図を示す。
a に対するbの強度はどれか。
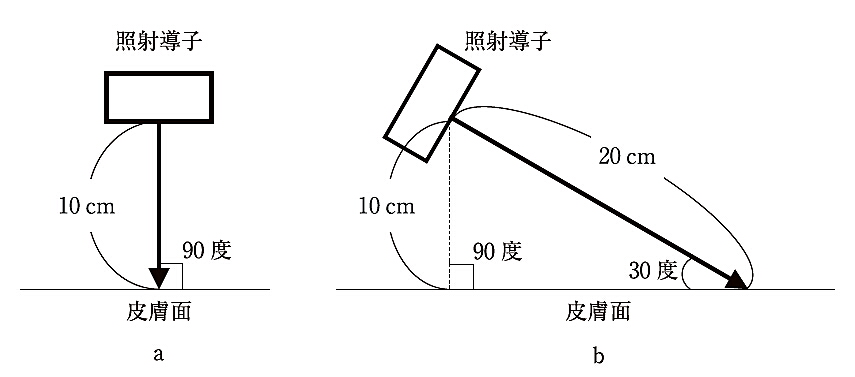
1. 1/2
2. 1/4
3. 1/6
4. 1/8
5. 1/16
【解説】
ランバートの余弦の法則を含んだ問題です。
ランベルトの余弦法則【Lambert’s cosine law】
完全に放散性の面から放出される光の強度は,面の法線と観測方向とのなす角度の余弦に比例している.ランベルトの放射の法則*,ランベルトの法則(反射光)*のように呼ぶこともある.(コトバンクによる)
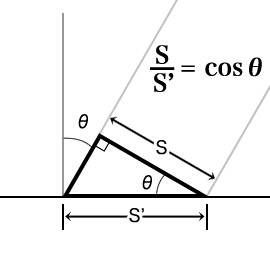
上の図をみてもらうと分かるように
S=S’×cosθ で
S’=S/cosθ
三角関数で考えると出てきます。
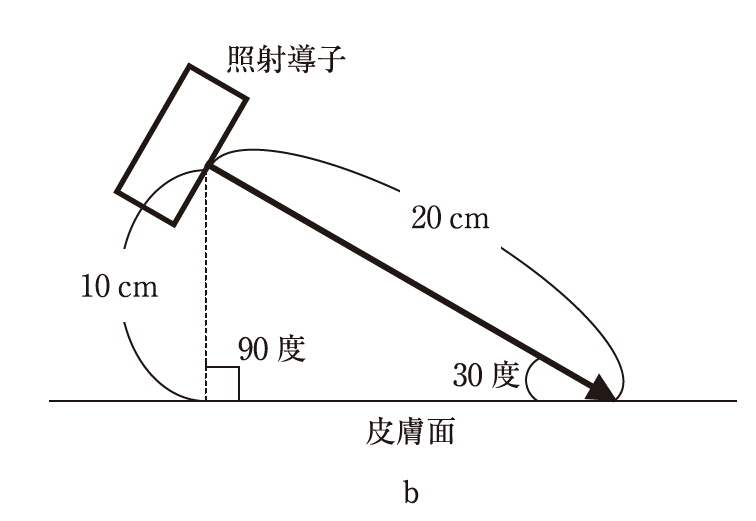
30度と60度の角度を持つ直角三角形の辺の比率は、決まっています。
1:√3:2 です!
上の図で当てはめると
1:√3:2=10:皮膚面:20
となります。
あまり当てはめる意味は、ありませんが・・・。
話を元に戻すと、
30度と60度の角度を持つ直角三角形の辺の比率から
cos30°=√3/2 となります。
cos60°=1/2 となります。
これは、お察しのとおり決まった値です。
それが、三角関数だからです。
ちなみに、皮膚面の長さは
1:√3:2=10:皮膚面:20 の比率が分かっていますので
1:√3=10:皮膚面 で計算すると
1×皮膚面=√3×10
皮膚面=√3×10 となります。
しかし、ここで注意!!
図をよく見比べてください!
θの示す場所は30°ですが、同じところを見ると
実は、60°なのです。(60度の角度で照射されていると考えてください。)

これは、直角(90度)から30度を引いた値です。
そのため、今回の国家試験問題では、
ランベルトの余弦法則に当てはめると
cos60°=1/2 を使うことになります。
こちらの方が、計算自体はやりやすいですね。
逆二乗の法則も使います。
照射量は、距離の2乗に反比例するというやつです。
すなわち、距離が2倍になるとその2乗の4に反比例しますので、
強さは1/4となります。
今回の問題でも、bの照射距離はa2倍になっています。
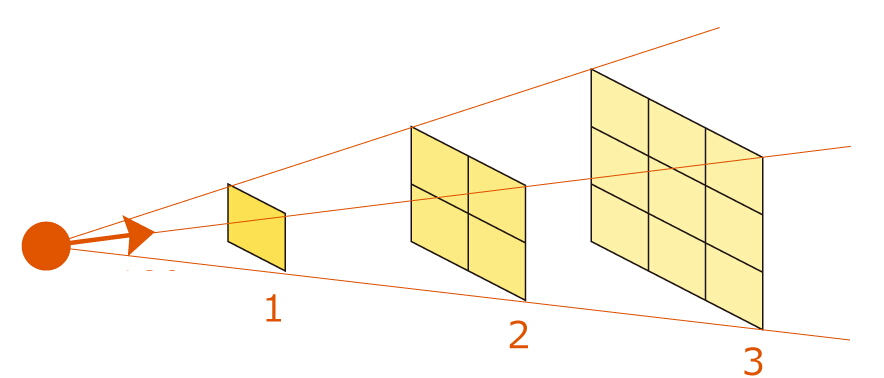
そのため、距離を考えると 1/4
角度を考えると 1/2
となります。
総合的には、この二つをかけ合わせますので
1/8となります。
答え
4. 1/8
