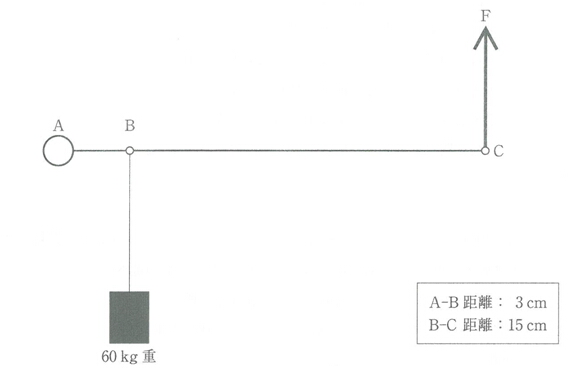
19 てこを図に示す。Aを支点とした棒のB点から60kg重の錘を糸で垂らした。棒を水平に支えるためにC点にかかる力F(N)はどれか。
ただし、1Nを100g重とし、棒と糸の質量は無視できるものとする。
1.60N
2.80N
3.90N
4.100N
5.120N
目次
【解説】
AB:BC=3:15(=1:5 となります。)
B地点に重りが負荷され、つり合っている状態であるため
(A地点にかかる負荷)+(C地点にかかる負荷)=60kg
比率から、全体の重量を1:5に分けて考えると、
ABの距離が短いため、つり合うためにはA地点はC地点よりも多くの力が必要となります。
距離の比率は、1:5となっているため、
1×(A地点に必要な力)=5×(C地点に必要な力)となります。
すなわち、全体の5/6がA地点に、1/6がC地点に必要な力となります。
そのため、C地点にかかる力(F)は、60/6となり、10kg重となります。
1N=100gと定義されており、10kg=10000gなので
10000/100=100Nとなります。
解答
4.100N
